Research

Published in Ph.D thesis, 2023

Abstract. Recent studies have brought to light profound connections between chemical reaction network theory and computer science, with the full scope of these relationships still emerging; however, the central Global Attractor Conjecture has remained open for over 50 years, preventing a full understanding of convergence in reaction networks.
We inroduce the class of simplicial reaction networks, applicable to a rich class of computational problems, and identify conditions sufficient to guarantee they adhere to well-controlled, predictable behaviors.

Simplicial reaction networks model processes on objects familiar to computer scientists and combinatorialists: spanning trees or matchings in a graph, vector spaces, matroids, and most generally, abstract simplicial complexes and the polytopes they define. The resulting reaction networks can thus be used to generate a distribution over large families of combinatorial objects that would often prove difficult to sample otherwise. In this way, we establish a method to harness the computational power of reaction networks to directly produce a desired distribution, in analogy with well-known Markov chain Monte Carlo methods.

We introduce a geometric method to analyze simplicial reaction networks based on
their associated polytopes, through the observation that points in these polytopes correspond precisely to different settings of invariants in the underlying reaction network. Through this method, we provide convergence results and proofs of the Global Attractor Conjecture for matroid, matching, and spanning tree reaction networks.

Published in Ph.D thesis, 2023

Abstract. We present a concise background on the state of the art in chemical reaction networks, and build on that prior work to generalize the known convergence results for so-called single linkage and strongly endotactic networks to a broader class of reaction networks. This improvement is accomplished in part through the organization of limiting behaviors into a partial order known as tiers. An idea from measurement theory provides a conceptual link to earlier works, showing that a per-species rather than per-complex analysis of tiers yields a stronger version of analogous results. We observe that, while earlier results necessarily fail to apply to reaction networks under downward closure, the new method presented in this thesis in combination with an invariant based linear programming algorithm succeeds in proving convergence results for some such networks.

In preparation, 2023

Abstract. The minimum rank problem for a graph takes as input a simple graph G = (V, E), whose vertices are identified to the index set {1, …, |V|}, and asks for the lowest possible rank among a class of |V| x |V| matrices related to the graph by their pattern of nonzero off-diagonal entries. We prove that the Minimum Rank problem, and in particular, the rank = 3 case, is complete for the existential theory of the reals (∃R). The minimum rank problem thus joins the ranks of problems which are complete for ∃R, which is known to be in PSPACE and NP-hard, and for which other known hard problems include training neural networks, recognizing intersection graphs of convex sets in the plane, and the algorithmic Steinitz problem.

We additionally show that, while a finite list of forbidden induced subgraphs is sufficient to characterize those graphs with minimum rank less than or equal to 2, and similarly some such list exists for any minimum rank d over finite fields, no such finite list is sufficient to characterize graphs of minimum rank 3 over the reals or over any infinite field.

With Alathea Jensen, Kevin Grace, and H. Tracy Hall

In Submission, 2022

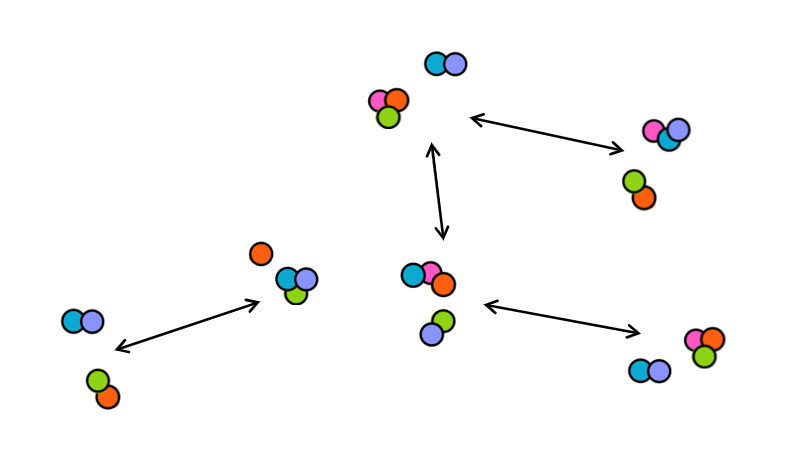
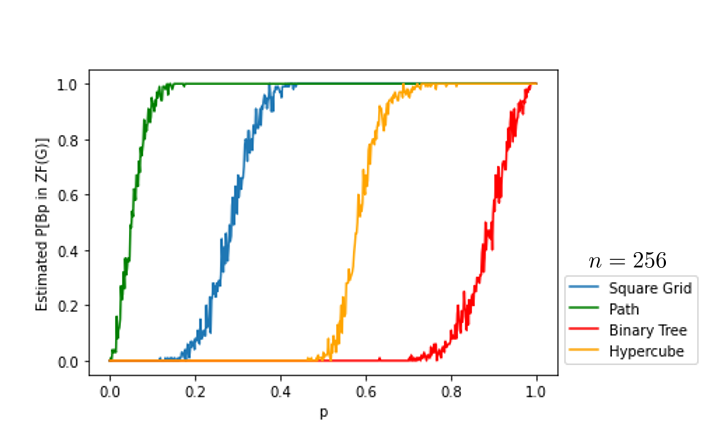
Abstract. Given a graph G and a real number 0≤p≤1, we define the random set Bp(G)⊂V(G) by including each vertex independently and with probability p. We investigate the probability that the random set Bp(G) is a zero forcing set of G. In particular, we prove that for large n, this probability for trees is upper bounded by the corresponding probability for a path graph. Given a minimum degree condition, we also prove a conjecture of Boyer et. al. regarding the number of zero forcing sets of a given size that a graph can have.

With Bryan Curtis, Luyining Gan, Jamie Haddock, Sam Spiro

Journal of Geometry, 2017

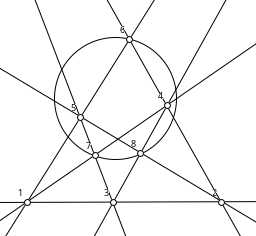
Abstract. An n-arc in a projective plane is a collection of n distinct points in the plane, no three of which lie on a line. Formulas counting the number of n-arcs in any finite projective plane of order q are known for n ≤ 8. In 1995, Iampolskaia, Skorobogatov, and Sorokin counted 9-arcs in the projective plane over a finite field of order q and showed that this count is a quasipolynomial function of q. We present a formula for the number of 9-arcs in any projective plane of order q, even those that are non-Desarguesian, deriving Iampolskaia, Skorobogatov, and Sorokin’s formula as a special case. We obtain our formula from a new implementation of an algorithm due to Glynn; we give details of our implementation and discuss its consequences for larger arcs.

With Nathan Kaplan, Susie Kimport, Luke Peilen, and Max Weinreich