Research
An incomplete list of interesting / public-facing projects from recent years.
LLMs and Automated Reasoning
Re-Imagine: Symbolic Benchmark Synthesis for Reasoning Evaluation
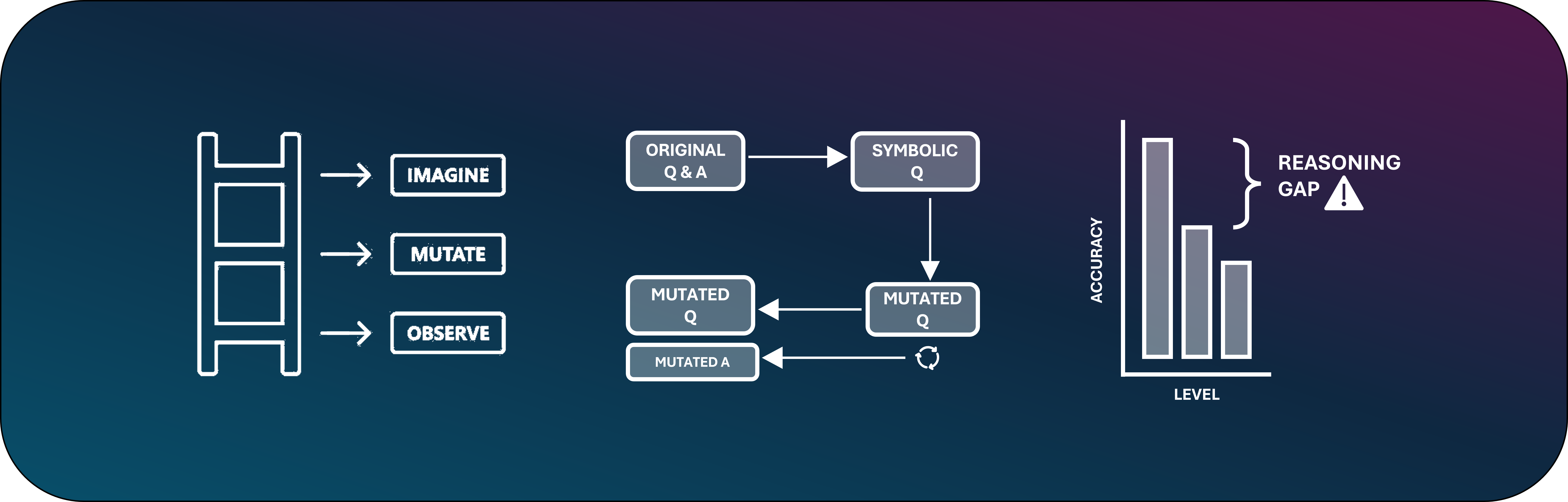
Recent Large Language Models (LLMs) have reported high accuracy on reasoning benchmarks. However, it is still unclear whether the observed results arise from true reasoning or from statistical recall of the training set. Inspired by the ladder of causation (Pearl, 2009) and its three levels (associations, interventions and counterfactuals), this paper introduces RE-IMAGINE, a framework to characterize a hierarchy of reasoning ability in LLMs, alongside an automated pipeline to generate problem variations at different levels of the hierarchy.
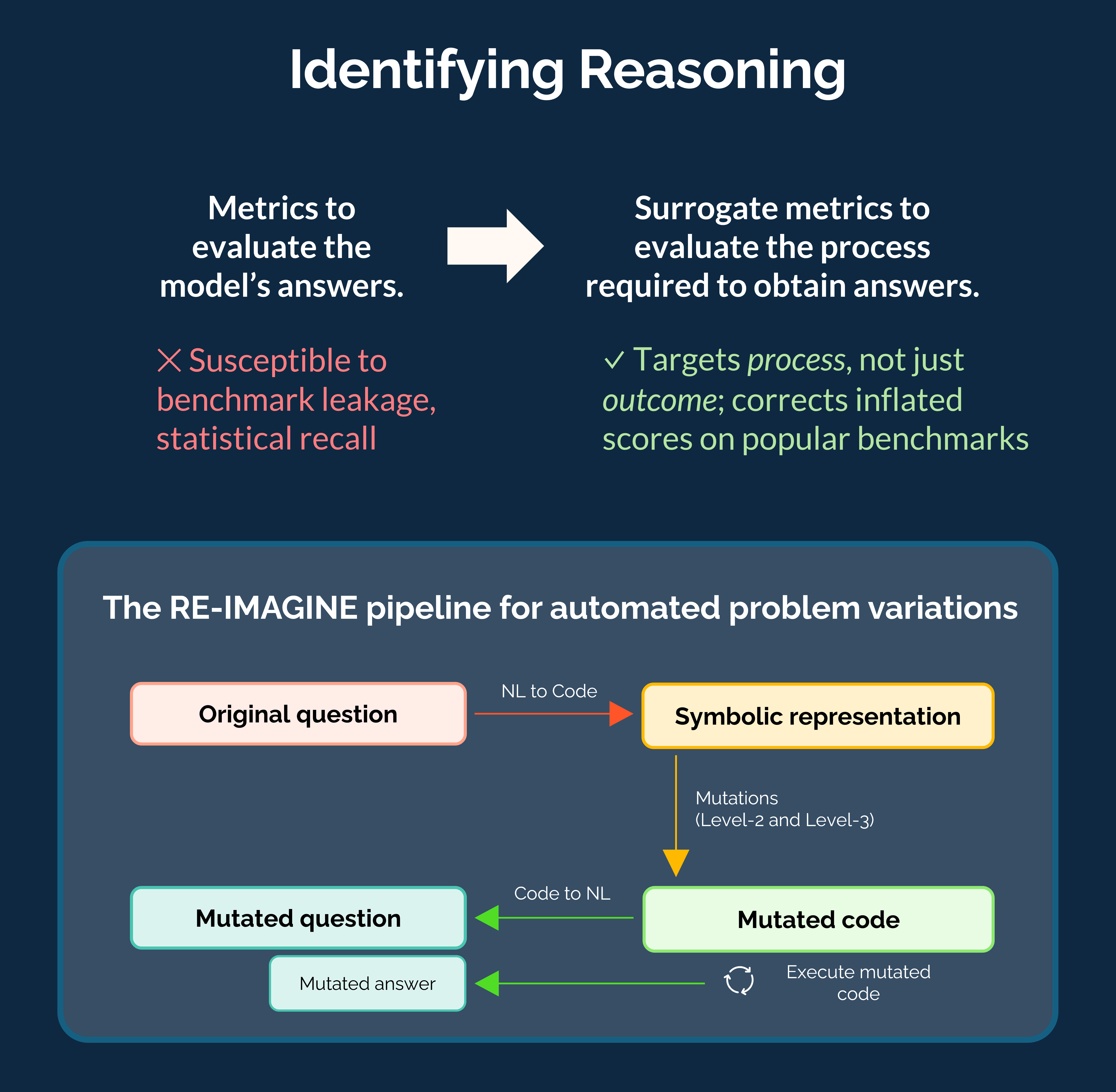
By altering problems in an intermediate symbolic representation, RE-IMAGINE generates arbitrarily many problems that are not solvable using memorization alone. Moreover, the framework is general and can work across reasoning domains, including math, code, and logic.
We demonstrate our framework on four widely-used benchmarks to evaluate several families of LLMs, and observe reductions in performance when the models are queried with problem variations. These assessments indicate a degree of reliance on statistical recall for past performance, and open the door to further research targeting skills across the reasoning hierarchy.
With Xinnuo Xu, Kshitij Dubey, Atharva Pandey, Risa Ueno, Fabian Falck, Aditya V Nori, Rahul Sharma, Amit Sharma, and Javier GonzalezICML 2025 Microsoft Research Blog Poster
Better Think Thrice: Learning to Reason Causally with Double Counterfactual Consistency
Beyond Reasoning Zombies -- AI Reasoning Requires Process Validity
Image Diffusion Models
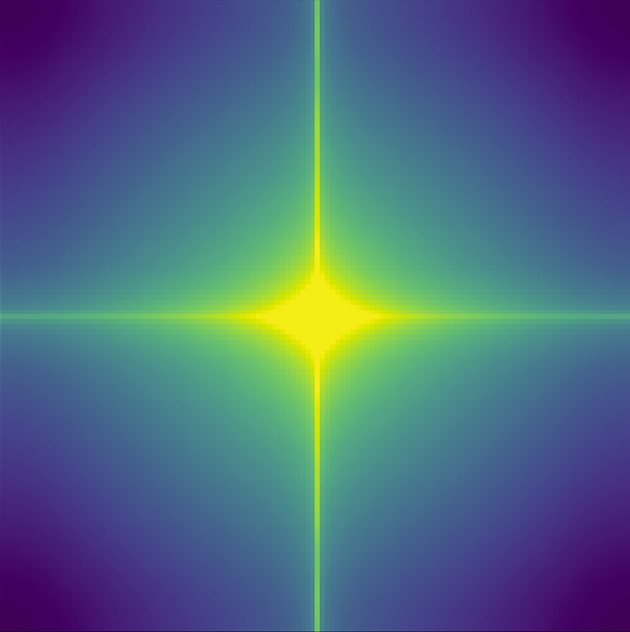
A Fourier Space Perspective on Diffusion Models
Diffusion models are state-of-the-art generative models on data modalities such as images, audio, proteins and materials. These modalities share the property of exponentially decaying variance and magnitude in the Fourier domain. Under the standard Denoising Diffusion Probabilistic Models (DDPM) forward process of additive white noise, this property results in high-frequency components being corrupted faster and earlier in terms of their Signal-to-Noise Ratio (SNR) than low-frequency ones. The reverse process then generates low-frequency information before high-frequency details. In this work, we study the inductive bias of the forward process of diffusion models in Fourier space. We theoretically analyse and empirically demonstrate that the faster noising of high-frequency components in DDPM results in violations of the normality assumption in the reverse process. Our experiments show that this leads to degraded generation quality of high-frequency components. We then study an alternate forward process in Fourier space which corrupts all frequencies at the same rate, removing the typical frequency hierarchy during generation, and demonstrate marked performance improvements on datasets where high frequencies are primary, while performing on par with DDPM on standard imaging benchmarks.
With Fabian Falck, Teodora Pandeva, Kiarash Zahirnia, Richard Turner, Edward Meeds, Javier Zazo, and Sushrut KarmalkarGraph Dynamical Systems
A fascinating cocktail of combinatorics, chemistry, and computation.
Simplicial Reaction Networks and the Global Attractor Conjecture
Recent studies have brought to light profound connections between chemical reaction network theory and computer science, with the full scope of these relationships still emerging; however, the central Global Attractor Conjecture has remained open for over 50 years, preventing a full understanding of convergence in reaction networks. We introduce the class of simplicial reaction networks, applicable to a rich class of computational problems, and identify conditions sufficient to guarantee they adhere to well-controlled, predictable behaviors.
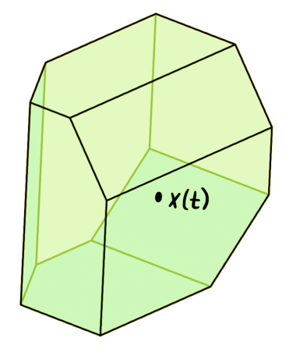
Simplicial reaction networks model processes on objects familiar to computer scientists and combinatorialists: spanning trees or matchings in a graph, vector spaces, matroids, and most generally, abstract simplicial complexes and the polytopes they define. The resulting reaction networks can thus be used to generate a distribution over large families of combinatorial objects that would often prove difficult to sample otherwise. In this way, we establish a method to harness the computational power of reaction networks to directly produce a desired distribution, in analogy with well-known Markov chain Monte Carlo methods.
We introduce a geometric method to analyze simplicial reaction networks based on their associated polytopes, through the observation that points in these polytopes correspond precisely to different settings of invariants in the underlying reaction network. Through this method, we provide convergence results and proofs of the Global Attractor Conjecture for matroid, matching, and spanning tree reaction networks.
Structural Conditions for Persistence in Quadratic Dynamical Systems
We present a concise background on the state of the art in chemical reaction networks and build on that prior work to generalize the known convergence results for so-called single linkage and strongly endotactic networks to a broader class of reaction networks. This improvement is accomplished in part through the organization of limiting behaviors into a partial order known as tiers. An idea from measurement theory provides a conceptual link to earlier works, showing that a per-species rather than per-complex analysis of tiers yields a stronger version of analogous results. We observe that, while earlier results necessarily fail to apply to reaction networks under downward closure, the new method presented in this thesis in combination with an invariant-based linear programming algorithm succeeds in proving convergence results for some such networks.
Inverse Eigenvalue Problems
From the matrix completion perspective:
Computational Complexity of the Minimum Rank Problem
The minimum rank problem for a graph takes as input a simple graph $G = (V, E)$, whose vertices are identified to the index set ${1, \ldots, |V|}$, and asks for the lowest possible rank among a class of |V| x |V| matrices related to the graph by their pattern of nonzero off-diagonal entries. We prove that the Minimum Rank problem, and in particular, the rank = 3 case, is complete for the existential theory of the reals ($\exists\mathbb{R}$). The minimum rank problem thus joins the ranks of problems which are complete for $\exists\mathbb{R}$, which is known to be in PSPACE and NP-hard, and for which other known hard problems include training neural networks, recognizing intersection graphs of convex sets in the plane, and the algorithmic Steinitz problem.
We additionally show that, while a finite list of forbidden induced subgraphs is sufficient to characterize those graphs with minimum rank less than or equal to 2, and similarly some such list exists for any minimum rank d over finite fields, no such finite list is sufficient to characterize graphs of minimum rank 3 over the reals or over any infinite field.
With Alathea Jensen, Kevin Grace, and H. Tracy HallAnd from the constraint propagation perspective:
Zero Forcing with Random Sets
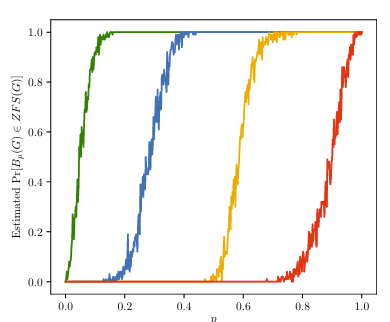
Given a graph $G$ and a real number $0\leq p\leq 1$, we define the random set $Bp(G)\subset V(G)$ by including each vertex independently and with probability $p$. We investigate the probability that the random set $Bp(G)$ is a zero forcing set of $G$. In particular, we prove that for large $n$, this probability for trees is upper bounded by the corresponding probability for a path graph. Given a minimum degree condition, we also prove a conjecture of Boyer et. al. regarding the number of zero forcing sets of a given size that a graph can have.
With Bryan Curtis, Luyining Gan, Jamie Haddock, Sam SpiroProjective Geometry
Counting Arcs in Projective Planes via Glynn's Algorithm
GitHub Journal of Geometry 2017
And, fascinatingly, finishing the story eight years later: